「ゼロから作るDeep Learning2ー自然言語処理編」DNNコードの中間層の2層化
少し調子に乗っているのかも知れませんが、「ディープラーニングそのものが分かったような気」になったので、「ゼロから作るDeep Learning 2 ―自然言語処理編」の全体が見えるようにしたDNNコードを少し書き換えてみます。どうしたのかというと、
中間層を2層にしてみました。
実際のコードがこちら、
「ゼロから作るDeep Learning 2 ―自然言語処理編」のDNNコード、P.45、第1章「1.4.3 学習用のソースコード」のimportをできるだけ外したものの中間層を2層化した
# ゼロから作る Deep Learning2のP45、第1章「1.4.3 学習用のソースコード」でコード全体が見えるようにできるだけ「import」を外したコード
# 中間層を1層追加して中間層を2層とする
# coding: utf-8
# import sys
# sys.path.append('..') # 親ディレクトリのファイルをインポートするための設定
import numpy as np
# from common.optimizer import SGD
# from dataset import spiral
import matplotlib.pyplot as plt
# from two_layer_net import TwoLayerNet
# ///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
# ///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
# コード変更、追加箇所の「開始」部分
# ///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
# +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
# functions.py の抜粋「開始」部分
# ---------------------------------------------------------------------------------------------------------------------------
def softmax(x):
if x.ndim == 2:
x = x - x.max(axis=1, keepdims=True)
x = np.exp(x)
x /= x.sum(axis=1, keepdims=True)
elif x.ndim == 1:
x = x - np.max(x)
x = np.exp(x) / np.sum(np.exp(x))
return x
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
# ---------------------------------------------------------------------------------------------------------------------------
# functions.py の抜粋「終了」部分
# +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
# +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
# optimizer.py の抜粋「開始」部分
# ---------------------------------------------------------------------------------------------------------------------------
class SGD:
'''
確率的勾配降下法(Stochastic Gradient Descent)
'''
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for i in range(len(params)):
params[i] -= self.lr * grads[i]
# ---------------------------------------------------------------------------------------------------------------------------
# optimizer.py の抜粋「終了」部分
# +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
# +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
# spiral.py の抜粋「開始」部分 エラーにうまく対処できず「load_data」をSpiralクラスに変更した
# ---------------------------------------------------------------------------------------------------------------------------
class Spiral:
def load_data(seed=1984):
np.random.seed(seed)
N = 100 # クラスごとのサンプル数
DIM = 2 # データの要素数
CLS_NUM = 3 # クラス数
x = np.zeros((N*CLS_NUM, DIM))
t = np.zeros((N*CLS_NUM, CLS_NUM), dtype=np.int64) # クラス化したらエラーとなったため「int」を「int64」に変更した
for j in range(CLS_NUM):
for i in range(N):#N*j, N*(j+1)):
rate = i / N
radius = 1.0*rate
theta = j*4.0 + 4.0*rate + np.random.randn()*0.2
ix = N*j + i
x[ix] = np.array([radius*np.sin(theta),
radius*np.cos(theta)]).flatten()
t[ix, j] = 1
return x, t
# ---------------------------------------------------------------------------------------------------------------------------
# spiral.py の抜粋「終了」部分
# +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
# +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
# three_layer_net.py の「開始」部分 中間層を2そうにしたため「two_layer_net.py」から変更した
# ---------------------------------------------------------------------------------------------------------------------------
class ThreeLayerNet:
def __init__(self, input_size, hidden_size, output_size):
I, H, O = input_size, hidden_size, output_size
# 重みとバイアスの初期化
W1 = 0.01 * np.random.randn(I, H)
b1 = np.zeros(H)
W2 = 0.01 * np.random.randn(H, H)
b2 = np.zeros(H)
W3 = 0.01 * np.random.randn(H, O) # 中間層を2層にしたための追加部分
b3 = np.zeros(O) # 中間層を2層にしたための追加部分
Sigmoid1 = Sigmoid() # 中間層を2層にしたための追加&名前変更部分
Sigmoid2 = Sigmoid() # 中間層を2層にしたための追加&名前変更部分
# レイヤの生成
self.layers = [
Affine(W1, b1),
Sigmoid1, # 中間層を2層にしたのために名前変更
Affine(W2, b2),
Sigmoid2, # 中間層を2層にしたための追加&名前変更部分
Affine(W3, b3) # 中間層を2層にしたための追加部分
]
self.loss_layer = SoftmaxWithLoss()
# すべての重みと勾配をリストにまとめる
self.params, self.grads = [], []
for layer in self.layers:
self.params += layer.params
self.grads += layer.grads
def predict(self, x):
for layer in self.layers:
x = layer.forward(x)
return x
def forward(self, x, t):
score = self.predict(x)
loss = self.loss_layer.forward(score, t)
return loss
def backward(self, dout=1):
dout = self.loss_layer.backward(dout)
for layer in reversed(self.layers):
dout = layer.backward(dout)
return dout
# ---------------------------------------------------------------------------------------------------------------------------
# three_layer_net.py の「終了」部分 「two_layer_net.py」から変更した
# +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
# +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
# layers.py の抜粋「開始」部分
# ---------------------------------------------------------------------------------------------------------------------------
class Affine:
def __init__(self, W, b):
self.params = [W, b]
self.grads = [np.zeros_like(W), np.zeros_like(b)]
self.x = None
def forward(self, x):
W, b = self.params
out = np.dot(x, W) + b
self.x = x
return out
def backward(self, dout):
W, b = self.params
dx = np.dot(dout, W.T)
dW = np.dot(self.x.T, dout)
db = np.sum(dout, axis=0)
self.grads[0][...] = dW
self.grads[1][...] = db
return dx
class Sigmoid:
def __init__(self):
self.params, self.grads = [], []
self.out = None
def forward(self, x):
out = 1 / (1 + np.exp(-x))
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dx
class SoftmaxWithLoss:
# ゼロつく1 P.156 の「SoftmaxWithLoss」とコード入れ替える
# 「https://www.anarchive-beta.com/entry/2020/08/05/180000」からコピペ
# 初期化メソッド
def __init__(self):
# 変数を初期化
self.loss = None # 交差エントロピー誤差
self.y = None # softmxの出力
self.t = None # 教師データ(one-hot vector)
# 順伝播メソッド
def forward(self, x, t):
# 教師ラベルを保存
self.t = t
# ソフトマックス関数による活性化(正規化)
self.y = softmax(x)
# 交差エントロピー誤差を計算
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
# 逆伝播メソッド
def backward(self, dout=1):
# バッチサイズを取得
batch_size = self.t.shape[0]
# 順伝播の入力の勾配を計算
dx = (self.y - self.t) / batch_size
return dx
# ---------------------------------------------------------------------------------------------------------------------------
# layers.py の抜粋「終了」部分
# +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
# ///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
# コード変更、追加箇所の「終了」部分
# ///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
# ///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
# ハイパーパラメータの設定
max_epoch = 500 # 中間層を2層にした関係で「300」から「500」へ変更
batch_size = 30
hidden_size = 20 # 中間層を2層にした関係で「10」から「20」へ変更
learning_rate = 2.0 # 中間層を2層にした関係で「1.0」から「2.0」へ変更
x, t = Spiral.load_data() # 「sprial」をクラス化したので先頭文字を大文字「Spiral」にした
model = ThreeLayerNet(input_size=2, hidden_size=hidden_size, output_size=3) # 中間層を2層にした関係で「TwoLayerNet」 から 「ThreeLayerNet」 へ変更した
optimizer = SGD(lr=learning_rate)
# 学習で使用する変数
data_size = len(x)
max_iters = data_size // batch_size
total_loss = 0
loss_count = 0
loss_list = []
for epoch in range(max_epoch):
# データのシャッフル
idx = np.random.permutation(data_size)
x = x[idx]
t = t[idx]
for iters in range(max_iters):
batch_x = x[iters*batch_size:(iters+1)*batch_size]
batch_t = t[iters*batch_size:(iters+1)*batch_size]
# 勾配を求め、パラメータを更新
loss = model.forward(batch_x, batch_t)
model.backward()
optimizer.update(model.params, model.grads)
total_loss += loss
loss_count += 1
# 定期的に学習経過を出力
if (iters+1) % 10 == 0:
avg_loss = total_loss / loss_count
# print('| epoch %d | iter %d / %d | loss %.2f'
# % (epoch + 1, iters + 1, max_iters, avg_loss))
loss_list.append(avg_loss)
total_loss, loss_count = 0, 0
# 学習結果のプロット
plt.plot(np.arange(len(loss_list)), loss_list, label='train')
plt.xlabel('iterations (x10)')
plt.ylabel('loss')
plt.show()
# 境界領域のプロット
h = 0.001
x_min, x_max = x[:, 0].min() - .1, x[:, 0].max() + .1
y_min, y_max = x[:, 1].min() - .1, x[:, 1].max() + .1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
X = np.c_[xx.ravel(), yy.ravel()]
score = model.predict(X)
predict_cls = np.argmax(score, axis=1)
Z = predict_cls.reshape(xx.shape)
plt.contourf(xx, yy, Z)
plt.axis('off')
# データ点のプロット
x, t = Spiral.load_data() # 「sprial」をクラス化したので先頭文字を大文字「Spiral」にした
N = 100
CLS_NUM = 3
markers = ['o', 'x', '^']
for i in range(CLS_NUM):
plt.scatter(x[i*N:(i+1)*N, 0], x[i*N:(i+1)*N, 1], s=40, marker=markers[i])
plt.show()
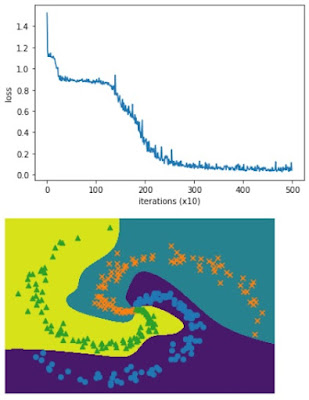
実行結果がこちら
ハイパーパラメータをいじることになったのですが、結果をみると、中間層2層化はうまくいったようです。
なお、コードの変更箇所は
「 # 中間層を2層にした・・・・・」
とコメントしたところなのでわかっていただけると思います。
2層化にあたっては、
”「ゼロから作るDeep Learning 2 ―自然言語処理編」のLSTMコード、P269、第6章「6.5.4 より良いRNNLMの実装」のコード
を参照しました。
以上です。



コメント
コメントを投稿