ディープラーニングのお勉強体験記”２７：GRUの２進数足算学習”（リカレントニューラルネットワーク”RNN”を中心にバックプロパゲーション”BPTT”を数式を使って理解したい！）

「ゼロから作るDeep Learning 2 ―自然言語処理編」のRNNコード、P216、第5章「5.5.3　RNNLMの学習コード」を使って作った「２進数足し算の学習コード」をGRUにする。

RNNのところで、P216、第5章「5.5.3　RNNLMの学習コード」に手を加えて、それを「２進数足し算の学習コード」にしましたが、それをGRUコードに作り替えました。

それがこれ！

P216、第5章「5.5.3　RNNLMの学習コード」を使った「２進数足し算の学習コード」をGRUに作り変えたコード

# ゼロから作る Deep Learning２のP216、第5章「5.5.3　RNNLMの学習コード」でコード全体が見えるようにできるだけ「import」を外した
# ２進数の計算をするコード　（入力データ、テストデータ共にコードでクラスから作成している）
# 中間層を1層追加して中間層を２層としたコード
# coding: utf-8
# import sys
# sys.path.append('C:\\kojin\\資料\\AI関連\\ゼロから作る Deep Learning\\ゼロから作る Deep Learning2\\deep-learning-from-scratch-2-master\\')
import matplotlib.pyplot as plt
import numpy as np
# from common.optimizer import SGD
# from dataset import ptb                 # このimportを有効にするには上記パス設定「sys.path.append('C:\\kojin\\AI関連\\・・・」が必要！
# from simple_rnnlm import SimpleRnnlm

# np.random.seed(seed=100)                       # 発生する乱数を固定する()

# ハイパーパラメータの設定
batch_size = 10
time_size = 10  # Truncated BPTTの展開する時間サイズ

n_in = 2    # 入力層のニューロン数
n_mid = 32  # 中間層のニューロン数
n_out = 1   # 出力層のニューロン数

# できるだけオリジナルのコードに変更を加えないため、既存の変数に代入する
vocab_size = n_out
wordvec_size = n_in
hidden_size = n_mid

lr = 0.01
max_epoch = 300

bin_data_len = 301     # ２進数のバッチ数を決める軸方向のデータ数

# 学習データの読み込み
# ------------------------------２進数学習用訓練データの作成-----------------------------------------
# +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
# ２進数データ作成CLASS「開始」部分
# ---------------------------------------------------------------------------------------------------------------------------
class Bin_data_make:

    def __init__(self, data_len = 100):
        self.data_len = data_len   
        self.list_bin_in = np.zeros((1,10,2))         # ２進数の計算用入力データの行列を初期設定
        self.list_bin_out = np.zeros((1,10,1))        # ２進数の計算用出力データの行列を初期設定

    def data_inout_set(self, ):

        for i in range(self.data_len):
            dec_in01 = int(500 * np.random.rand())    # ２進数の計算入力データ作成用１０進数　１番
            dec_in02 = int(500 * np.random.rand())    # ２進数の計算入力データ作成用１０進数　２番
            dec_out = dec_in01 + dec_in02             # ２進数の計算出力データ作成用１０進数
    
            bin_in01 = np.array(list(map(int, format(dec_in01, '010b')))) # １０進数を2進数を変換　入力１番
            bin_in02 = np.array(list(map(int, format(dec_in02, '010b')))) # １０進数を2進数を変換　入力２番
            bin_out = np.array(list(map(int, format(dec_out, '010b'))))   # １０進数を2進数を変換　出力

            in01 = bin_in01.reshape(1, 10)     # ２進数の計算入力データを2次元行列にする　１番
            in02 = bin_in02.reshape(1, 10)     # ２進数の計算入力データを2次元行列にする　２番
            out00 = bin_out.reshape(1, 10)     # ２進数の計算出力データを2次元行列にする
    
            list_in01 = np.append(in01, in02, axis=0)  # ２進数の計算入力データを１つの行列に合わせる
            list_in02 = np.rot90(list_in01, k=1)       # ２進数の１つの行列に合わせたものを回転する
            list_in00 = list_in02.reshape(1,10,2)      # バッチ化するため回転した行列を3次元行列にする

            list_out = np.rot90(out00, k=1)          # ２進数の１つの行列に合わせたものを回転する
            list_out = list_out.reshape(1,10,1)      # バッチ化対応で回転した行列を3次元行列にする

            self.list_bin_in = np.append(self.list_bin_in, list_in00, axis=0)        # ２進数の入力データ
            self.list_bin_out = np.append(self.list_bin_out, list_out, axis=0)       # ２進数の出力データ

        return self.list_bin_in, self.list_bin_out
# ---------------------------------------------------------------------------------------------------------------------------
# ２進数データ作成CLASS「終了」部分
# +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
#------------------------------------------------------------------------------------------------

bin_train_data = Bin_data_make(bin_data_len)
x_tarin_data, t_tarin_data = bin_train_data.data_inout_set()

xs = x_tarin_data[1:]  # 入力              ２進数の先頭データは「０」ベクトルのため削除する
ts = t_tarin_data[1:]  # 出力（教師ラベル）  ２進数の先頭データは「０」ベクトルのため削除する
data_size = len(xs)

# 学習時に使用する変数
# max_iters = data_size // (batch_size * time_size)
max_iters = data_size // batch_size               # 2進数足し算学習のデータ量として、「time_size」で割ってしまうと足りなくなる
time_idx = 0
total_loss = 0
loss_count = 0
ppl_list = []


# ///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
# ///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
# できるだけimportを外すため、classをコピペした箇所の「開始」部分
# ///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////

# GPUを定義しておく（コードのどこかでこの定義を参照しているらしいけど、PCにNVIDIA無いので、下記定義をするだけ）
GPU = False

# +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
# optimizer.py の抜粋「開始」部分
# ---------------------------------------------------------------------------------------------------------------------------
class SGD:
    '''
    確率的勾配降下法（Stochastic Gradient Descent）
    '''
    def __init__(self, lr=0.01):
        self.lr = lr
        
    def update(self, params, grads):
        for i in range(len(params)):
            params[i] -= self.lr * grads[i]
# ---------------------------------------------------------------------------------------------------------------------------
# optimizer.py の抜粋「終了」部分
# +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

# +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
# functions.py の全部抜粋「開始」部分
# ---------------------------------------------------------------------------------------------------------------------------
def sigmoid(x):
    return 1 / (1 + np.exp(-x))
# ---------------------------------------------------------------------------------------------------------------------------
# functions.py の全部抜粋「終了」部分
# +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

# +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
# time_layers.py の抜粋「開始」部分
# ---------------------------------------------------------------------------------------------------------------------------
class TimeAffine:
    def __init__(self, W, b):
        self.params = [W, b]
        self.grads = [np.zeros_like(W), np.zeros_like(b)]
        self.x = None

    def forward(self, x):
        N, T, D = x.shape
        W, b = self.params

        rx = x.reshape(N*T, -1)
        out = np.dot(rx, W) + b
        self.x = x
        return out.reshape(N, T, -1)

    def backward(self, dout):
        x = self.x
        N, T, D = x.shape
        W, b = self.params

        dout = dout.reshape(N*T, -1)
        rx = x.reshape(N*T, -1)

        db = np.sum(dout, axis=0)
        dW = np.dot(rx.T, dout)
        dx = np.dot(dout, W.T)
        dx = dx.reshape(*x.shape)

        self.grads[0][...] = dW
        self.grads[1][...] = db

        return dx

class GRU:
    def __init__(self, Wx, Wh, b):
        '''
        Parameters
        ----------
        Wx: 入力`x`用の重みパラーメタ（3つ分の重みをまとめる）
        Wh: 隠れ状態`h`用の重みパラメータ（3つ分の重みをまとめる）
        b: バイアス（3つ分のバイアスをまとめる）
        '''
        self.params = [Wx, Wh, b]
        self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
        self.cache = None

    def forward(self, x, h_prev):
        Wx, Wh, b = self.params
        H = Wh.shape[0]
        Wxz, Wxr, Wxh = Wx[:, :H], Wx[:, H:2 * H], Wx[:, 2 * H:]
        Whz, Whr, Whh = Wh[:, :H], Wh[:, H:2 * H], Wh[:, 2 * H:]
        bz, br, bh = b[:H], b[H:2 * H], b[2 * H:]

        z = sigmoid(np.dot(x, Wxz) + np.dot(h_prev, Whz) + bz)
        r = sigmoid(np.dot(x, Wxr) + np.dot(h_prev, Whr) + br)
        h_hat = np.tanh(np.dot(x, Wxh) + np.dot(r*h_prev, Whh) + bh)
        h_next = (1-z) * h_prev + z * h_hat

        self.cache = (x, h_prev, z, r, h_hat)

        return h_next

    def backward(self, dh_next):
        Wx, Wh, b = self.params
        H = Wh.shape[0]
        Wxz, Wxr, Wxh = Wx[:, :H], Wx[:, H:2 * H], Wx[:, 2 * H:]
        Whz, Whr, Whh = Wh[:, :H], Wh[:, H:2 * H], Wh[:, 2 * H:]
        x, h_prev, z, r, h_hat = self.cache

        dh_hat =dh_next * z
        dh_prev = dh_next * (1-z)

        # tanh
        dt = dh_hat * (1 - h_hat ** 2)
        dbh = np.sum(dt, axis=0)
        dWhh = np.dot((r * h_prev).T, dt)
        dhr = np.dot(dt, Whh.T)
        dWxh = np.dot(x.T, dt)
        dx = np.dot(dt, Wxh.T)
        dh_prev += r * dhr

        # update gate(z)
        dz = dh_next * h_hat - dh_next * h_prev
        dt = dz * z * (1-z)
        dbz = np.sum(dt, axis=0)
        dWhz = np.dot(h_prev.T, dt)
        dh_prev += np.dot(dt, Whz.T)
        dWxz = np.dot(x.T, dt)
        dx += np.dot(dt, Wxz.T)

        # rest gate(r)
        dr = dhr * h_prev
        dt = dr * r * (1-r)
        dbr = np.sum(dt, axis=0)
        dWhr = np.dot(h_prev.T, dt)
        dh_prev += np.dot(dt, Whr.T)
        dWxr = np.dot(x.T, dt)
        dx += np.dot(dt, Wxr.T)

        self.dWx = np.hstack((dWxz, dWxr, dWxh))
        self.dWh = np.hstack((dWhz, dWhr, dWhh))
        self.db = np.hstack((dbz, dbr, dbh))

        self.grads[0][...] = self.dWx
        self.grads[1][...] = self.dWh
        self.grads[2][...] = self.db

        return dx, dh_prev

class TimeGRU:
    def __init__(self, Wx, Wh, b, stateful=False):
        self.params = [Wx, Wh, b]
        self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
        self.layers = None
        self.h, self.dh = None, None
        self.stateful = stateful

    def forward(self, xs):
        Wx, Wh, b = self.params
        N, T, D = xs.shape
        H = Wh.shape[0]
        self.layers = []
        hs = np.empty((N, T, H), dtype='f')

        if not self.stateful or self.h is None:
            self.h = np.zeros((N, H), dtype='f')

        for t in range(T):
            layer = GRU(*self.params)
            self.h = layer.forward(xs[:, t, :], self.h)
            hs[:, t, :] = self.h
            self.layers.append(layer)
        return hs

    def backward(self, dhs):
        Wx, Wh, b = self.params
        N, T, H = dhs.shape
        D = Wx.shape[0]

        dxs = np.empty((N, T, D), dtype='f')

        dh = 0
        grads = [0, 0, 0]
        for t in reversed(range(T)):
            layer = self.layers[t]
            dx, dh = layer.backward(dhs[:, t, :] + dh)
            dxs[:, t, :] = dx

            for i, grad in enumerate(layer.grads):
                grads[i] += grad

        for i, grad in enumerate(grads):
            self.grads[i][...] = grad

        self.dh = dh
        return dxs

    def set_state(self, h):
        self.h = h

    def reset_state(self):
        self.h = None

class TimeOutputWithLoss:
# このコードは「class TimeSoftmaxWithLoss」の代わりに実装する

    def __init__(self):
        self.cache = None

    def forward(self, xs, ts):
        N, T, D = xs.shape # ここでDは1

# RNNのタイプに合わせて「#1」か「#2」を選択する
        # ------------------RNN many to many start---------------#1
        loss = 0.5 * np.sum((xs - ts)**2)                        #1
        loss /= N # 1データ分での誤差                              #1
        # -------------------RNN many to many end----------------#1

#        # ------------------RNN many to one start----------------#2
#        loss = 0.5 * np.sum((xs[:, T-1, :] - ts[:, T-1, :])**2)  #2
#        loss /= N # 1データ分での誤差                              #2
#        # -------------------RNN many to one end-----------------#2
     
        self.cache = (ts, xs, (N, T, D))

        return loss

    def backward(self, dout=1):
        ts, xs, (N, T, D) = self.cache

# RNNのタイプに合わせて「#1」か「#2」を選択する
        # ------------------RNN many to many start---------------#1
        dout = xs - ts                                           #1
        dout /= N                                                #1
        # -------------------RNN many to many end----------------#1

#        # ------------------RNN many to one start----------------#2
#        dout = np.zeros([N, T, D], dtype='float')                #2
#        dout[:, T-1, :] = xs[:, T-1, :] - ts[:, T-1, :]          #2
#        # -------------------RNN many to one end-----------------#2
        
        return dout
# ---------------------------------------------------------------------------------------------------------------------------
# time_layers.py の抜粋「終了」部分
# +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

# +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
# simple_rnnlm.py の抜粋「開始」部分
# ---------------------------------------------------------------------------------------------------------------------------
class SimpleRnnlm:
    def __init__(self, vocab_size, wordvec_size, hidden_size):
        V, D, H = vocab_size, wordvec_size, hidden_size
        rn = np.random.randn

        # 重みの初期化
#        embed_W = (rn(V, D) / 100).astype('f')                    # embedingレイヤは無効にする
        gru_Wx1 = (rn(D, 3 * H) / np.sqrt(D)).astype('f')       # 「lstm」を「gru」に書き換えつつ、「4」を「3」にした 中間層を1層追加して「３Layer」に変更するために名前変更
        gru_Wh1 = (rn(H, 3 * H) / np.sqrt(H)).astype('f')       # 「lstm」を「gru」に書き換えつつ、「4」を「3」にした 中間層を1層追加して「３Layer」に変更するために名前変更
        gru_b1 = np.zeros(3 * H).astype('f')                    # 「lstm」を「gru」に書き換えつつ、「4」を「3」にした 中間層を1層追加して「３Layer」に変更するために名前変更
        gru_Wx2 = (rn(H, 3 * H) / np.sqrt(H)).astype('f')       # 「lstm」を「gru」に書き換えつつ、「4」を「3」にした 中間層を1層追加して「３Layer」に変更するために追加したコード
        gru_Wh2 = (rn(H, 3 * H) / np.sqrt(H)).astype('f')       # 「lstm」を「gru」に書き換えつつ、「4」を「3」にした 中間層を1層追加して「３Layer」に変更するために追加したコード
        gru_b2 = np.zeros(3 * H).astype('f')                    # 「lstm」を「gru」に書き換えつつ、「4」を「3」にした 中間層を1層追加して「３Layer」に変更するために追加したコード
        affine_W = (rn(H, V) / np.sqrt(H)).astype('f')
        affine_b = np.zeros(V).astype('f')

        # レイヤの生成
        self.layers = [
#            TimeEmbedding(embed_W),                               # embedingレイヤは無効にする
            TimeGRU(gru_Wx1, gru_Wh1,gru_b1, stateful=True),    # 中間層を1層追加して「３Layer」に変更するために名前変更
            TimeGRU(gru_Wx2, gru_Wh2,gru_b2, stateful=True),    # 中間層を1層追加して「３Layer」に変更するために追加したコード
            TimeAffine(affine_W, affine_b)
        ]

#        self.loss_layer = TimeSoftmaxWithLoss()                   # TimeSoftmaxWithLossレイヤは無効にする
        self.loss_layer = TimeOutputWithLoss()
        self.rnn_layer = self.layers[0]                            # 「TimeEmbedding」を外したので「TimeRNN」を「self.rnn_layer」にするため「self.layers[1]」を「self.layers[0]」にした

        # すべての重みと勾配をリストにまとめる
        self.params, self.grads = [], []
        for layer in self.layers:
            self.params += layer.params
            self.grads += layer.grads

#------オリジナルコードに予測（predict）が無いので、LSTMのコードから持ってくる------
    def predict(self, xs):
        for layer in self.layers:
            xs = layer.forward(xs)
        return xs

    def forward(self, xs, ts):
        for layer in self.layers:
            xs = layer.forward(xs)
        loss = self.loss_layer.forward(xs, ts)
        return loss

    def backward(self, dout=1):
        dout = self.loss_layer.backward(dout)
        for layer in reversed(self.layers):
            dout = layer.backward(dout)
        return dout

    def reset_state(self):
        self.rnn_layer.reset_state()
# ---------------------------------------------------------------------------------------------------------------------------
# simple_rnnlm.py の抜粋「終了」部分
# +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

# ///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
#  できるだけimportを外すため、classをコピペした箇所の「終了」部分
# ///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
# ///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////


# モデルの生成
model = SimpleRnnlm(vocab_size, wordvec_size, hidden_size)
optimizer = SGD(lr)

# ミニバッチの各サンプルの読み込み開始位置を計算
# jump = time_size
# offset = [i * jump for i in range(batch_size)]

for epoch in range(max_epoch):

    #---「common」の「trainer.py」から「class Trainer」よりデータをシャッフルする部分を抜粋---
    # time_idx = 0                                 # インデックス追加部分
    # シャッフル
    idx = np.random.permutation(np.arange(data_size))
    x_shuffle = xs[idx, ]
    t_shuffle = ts[idx, ]
    #-----------------------------------------------------------------------------------
    
# /////////////////////////////////////////////////////////////////////////////////////////////////////////
    for iter in range(max_iters - 1):
        # ミニバッチの取得

        batch_x = np.empty((batch_size, time_size, wordvec_size), dtype='f')
        batch_t = np.empty((batch_size, time_size, vocab_size), dtype='f')

        for i in range(batch_size):
            batch_x[i, :, :] = x_shuffle[i,: ,:]
            batch_t[i, :, :] = t_shuffle[i,: ,:]
#            batch_x[i, :, :] = x_reshape[i + batch_size * iter ,: , :]
#            batch_t[i, :, :] = t_reshape[i + batch_size * iter ,: , :]
#        time_idx += batch_size

# /////////////////////////////////////////////////////////////////////////////////////////////////////////

        # 勾配を求め、パラメータを更新
        loss = model.forward(batch_x, batch_t)
        model.backward()
        optimizer.update(model.params, model.grads)
        total_loss += loss
        loss_count += 1
    # エポックごとにパープレキシティの評価　　　　　　　　　「パープレキシティ」はここでは「ロス」として扱う
#    ppl = np.exp(total_loss / loss_count)
    ppl = total_loss
#    print('| epoch %d | perplexity %.2f'
#          % (epoch+1, ppl))
    ppl_list.append(float(ppl))
    total_loss, loss_count = 0, 0

#----------------予測部分開始-------------------------------------
#-------------------2進数データをコードで作成-----------------------
test_bin_data_len = batch_size

#----------------２進数の予測テータをクラスから作成------------------
bin_test_data = Bin_data_make(test_bin_data_len)
x_test_data, t_test_data = bin_test_data.data_inout_set()

x_reshape_td = x_test_data[1:]     #２進数の先頭データは「０」ベクトルのため削除する
t_reshape_td = t_test_data[1:]     #２進数の先頭データは「０」ベクトルのため削除する

# -- 予測 --
    # 順伝播 RNN層
y_predict_td = np.empty((batch_size,  time_size, vocab_size), dtype='f')      

y_predict_td = model.predict(x_reshape_td) 
#-----------------予測部分終了------------------------------------

# グラフの描画　誤差の表示部分
x = np.arange(len(ppl_list))
plt.plot(x, ppl_list, label='train')
plt.xlabel('epochs')
plt.ylabel('loss')
plt.show()

# 2進数の予測結果を表示
#print('y_predict_td, x_reshape_td, t_reshape_td = {},{},{}'.format(y_predict_td, x_reshape_td, t_reshape_td)) 

# グラフの描画　学習結果の波形パターンの一致度合いを表示
height1 = t_reshape_td[0:9].reshape(-1)  # 正解データ 　指定した分データを抜粋する
height2 = y_predict_td[0:9].reshape(-1)  # 予測データ 　指定した分データを抜粋する
x = np.arange(len(height1))  # numpyで横軸を設定

plt.plot(x, height1, height2, label='train')
plt.xlabel('data number')
plt.ylabel('binary answer')
plt.show()
 

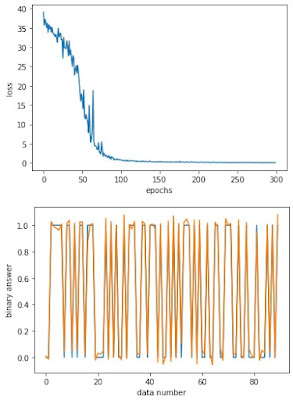
実行結果がこれ！

問題なさそうです。

RNNからGRUへ変更するために書き換えたところはLSTMで書き換えたところとほぼ同じです。

このグラフの内容に関しては

”「ゼロから作るDeep Learning 2 ―自然言語処理編」のRNNコード、P216、第5章「5.5.3　RNNLMの学習コード」を使って「２進数足し算の学習コード」を作る”

を参照してください。

以上です。